3 Leis Matemáticas para aprender em Ciência de Dados
Além de Tecnologia, Programação e Análise de Dados, conhecer algumas Leis Matemáticas é fundamental para o Cientista de Dados. Veja 3 aqui!
Autor: Redação Impacta
Um cientista de dados necessita de conhecimentos em programação e tecnologia no dia a dia da sua profissão. Mas a matemática na ciência de dados também possui sua importância e um profissional da área precisa conhecer alguns conceitos.
Por isso, vamos explicar quais são as três leis matemáticas essenciais para um cientista de dados conhecer para atuar na área. Acompanhe!
Qual a importância da matemática para a ciência de dados?
A ciência de dados se fundamenta em diversas normas e conceitos matemáticos. Um cientista de dados vai precisar de conhecimentos em teorias estatísticas e de probabilidade para fazer a correta análise e compreender os dados estudados.
Pode-se inclusive falar que o sucesso de um cientista de dados está justamente na capacidade dele de utilizar os conhecimentos matemáticos na análise dos dados.
Mesmo que a matemática não seja o único conhecimento exigido para ser um cientista de dados, com certeza é um dos mais importantes e necessários.
Conheça as principais leis matemáticas na ciência de dados
Existem muitas leis matemáticas que são utilizadas na ciência de dados, principalmente as que envolvem estatísticas e probabilidade.
No entanto escolhemos dentre todas, as três leis matemáticas que todo cientista de dados precisa conhecer.
Lei de Benford
A lei de Benford ou lei do primeiro dígito, como também é conhecida, é uma das leis matemáticas úteis no trabalho de um cientista de dados. A lei dispõe sobre a probabilidade de coleções de números aparecerem.
As primeiras ideias da lei foram feitas pelo astrônomo canadense Simon Newcomb, ainda em 1881. Durante a leitura de um livro de logaritmo, ele percebeu que as primeiras folhas estavam mais gastas que as demais. A “coincidência” também ocorria em outros tipos de livros.
No entanto, a lei se popularizou somente após os estudos do físico americano Frank Benford em 1938, que revisitou as teorias de Simon. Justamente por isso a lei recebeu o sobrenome de Frank.
Benford analisou 20 contextos diferentes e encontrou a mesma “coincidência”. Ele descobriu que existia um padrão em números como tamanho da população, mortalidade, extensão de rios, entre outros.
De acordo com as descobertas de Benford se formulou a lei do primeiro dígito. A lei diz que a chance do primeiro dígito de um número ser um é maior do que a de ser dois e assim por diante.
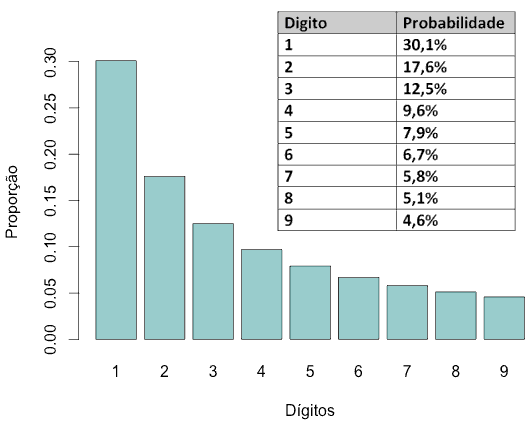
A lei inclusive possui uma tabela exemplificando a frequência dos 9 algarismos. Segundo a tabela, o algarismo 1 tem 30% de chance de ser o primeiro dígito de um número, enquanto a chance do 2 é de 17,6%.
A porcentagem vai diminuindo progressivamente até o algarismo 9 que possui apenas 4,6% de chance de ser o primeiro dígito.
A lei de Benford pode ser utilizada para revelar fraudes contábeis, apurar dados eleitorais ou calcular indicadores econômicos.
Inclusive, várias iniciativas se utilizaram da lei do primeiro dígito para conferir a veracidade dos dados sobre a evolução da pandemia no Brasil e no mundo.
Lei dos grandes números
A lei dos grandes números (LGN) é o teorema fundamental das teorias da probabilidade. A lei descreve que ao realizar uma experiência repetidas vezes, mais perto se fica de chegar ao resultado esperado.
Foi primeiramente proposta pelo matemático italiano Girolamo Cardano (1501 – 1567), contudo este não apresentou na época provas convincentes. Apenas anos depois, o matemático suíço Jakob Bernoulli (1654-1705) conseguiu comprovar a veracidade da teoria.
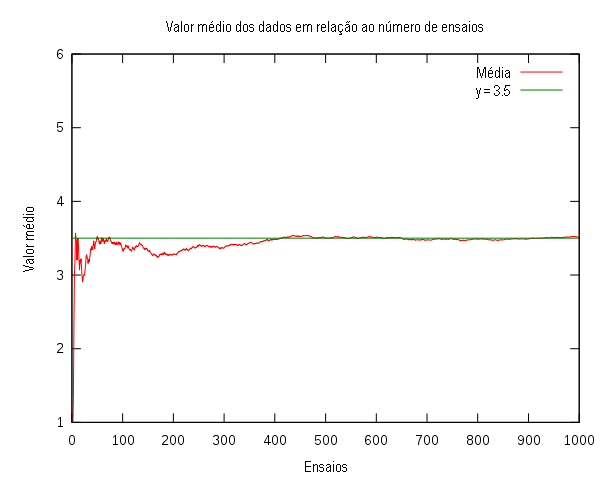
Como dito no início do tópico, de acordo com a lei dos grandes números, ao se analisar uma variável X repetidas vezes é possível chegar cada vez mais perto do valor esperado da mesma.
Pode parecer um pouco confuso em um primeiro momento, porém com uma exemplificação as coisas ficam mais compreensíveis.
Então, podemos utilizar o exemplo de uma moeda sendo jogada. Existem duas possibilidades, cara ou coroa, o que significa que ambas as variáveis possuem um valor esperado de 50%. Contudo, nem sempre as jogadas mostram essa proporção em um primeiro momento.
Os resultados das jogadas podem repetir-se por algumas tentativas, por exemplo, pode aparecer coroa em quatro de cinco jogadas consecutivas. Portanto a proporção se afasta bastante do valor esperado, ficando em 75% para coroa.
Mas, considerando a lei dos grandes números, se repetirmos várias vezes e tirarmos a média, ela irá se aproximar do valor esperado.
Pelos cientistas de dados, a lei dos grandes números pode ser utilizada para a realização de cálculos financeiros, demográficos e também na inteligência artificial.
Lei de Zipf
Outra das leis matemáticas na ciência de dados é a lei de Zipf. Ela recebe este nome em homenagem ao linguista americano George Kingsley Zipf.
Apesar de que ele não afirmasse tê-la criado, ele foi o responsável por sua popularização e por apresentar explicações acerca da mesma.
A lei de Zipf é uma lei de potências sobre a distribuição de valores de acordo com o número de ordem numa lista.
Em palavras simples, a lei diz que o segundo elemento de uma lista se repetirá aproximadamente com uma frequência que é correspondente à metade do primeiro, por sua vez o terceiro se repetirá com um terço da frequência do primeiro, e assim por diante.
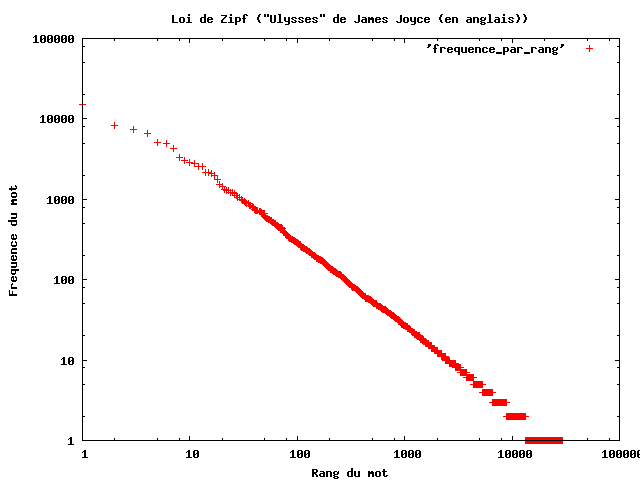
Zipf fez seus estudos analisando a obra literária “Ulisses” de James Joyce (gráfico acima), contando e ordenando por frequências as palavras do livro.
Os resultados demonstraram que a palavra mais comum apareceu 8000 vezes, já a décima, 800 vezes e a milésima apenas 8 vezes.
Com a lei de Zipf foi possível definir a palavra mais comum na língua inglesa, o artigo “the”.
Mas muito além de apenas demonstrar as palavras mais utilizadas, a lei pode ser utilizada na ciência de dados, por exemplo, para fazer análises de sentimentos em redes sociais, classificação de textos e também é bastante comum em indicadores demográficos.
Conclusão
Como foi possível perceber, as leis matemáticas na ciência de dados cumprem papel fundamental e podem ser usadas em várias análises de dados.
Entre as várias, podemos citar as Leis de Benford, Grande Números e Zipf como as mais importantes para o trabalho de cientista de dados. Conhecê-las é de suma importância para esses profissionais.
Assim como é importante conhecer as leis matemáticas na ciência de dados, saber conceitos de programação também é essencial.
Tem interesse e fazer carreira em análise de dados, ciência de dados e administração de bancos de dados, contribuindo para a tomada de decisões e transformação digital nas organizações? Na Impacta temos a graduação certa para você. Clique aqui e saiba mais!
Deixe o seu comentário!